
Modify the previous example to create the same fits using workspace Observe the specified c constants % do not make a good fit. % Call fit again and specify a different value of c, % to get a new fit.į2 = fit( xdata, ydata, g, 'problem', 1, 'start', ) % Note: Specify start points in the calls to fit to % avoid warning messages about random start points % and to ensure repeatability of results. Observe that c is an argument.į1 = fit( xdata, ydata, g, 'problem', 0, 'StartPoint', ) % Create a fittype that has a problem parameter. Interpn Multidimensional data interpolation (table lookup) Interp3 Three-dimensional data interpolation (table lookup) Interp2 Two-dimensional data interpolation (table lookup) See Also interpft One-dimensional interpolation using the FFT method. For access to the more advanced features, see these M-files and the Spline Toolbox. spline uses them in a fairly simple fashion to perform cubic spline interpolation. These routines form a small suite of functions for working with piecewise polynomials.
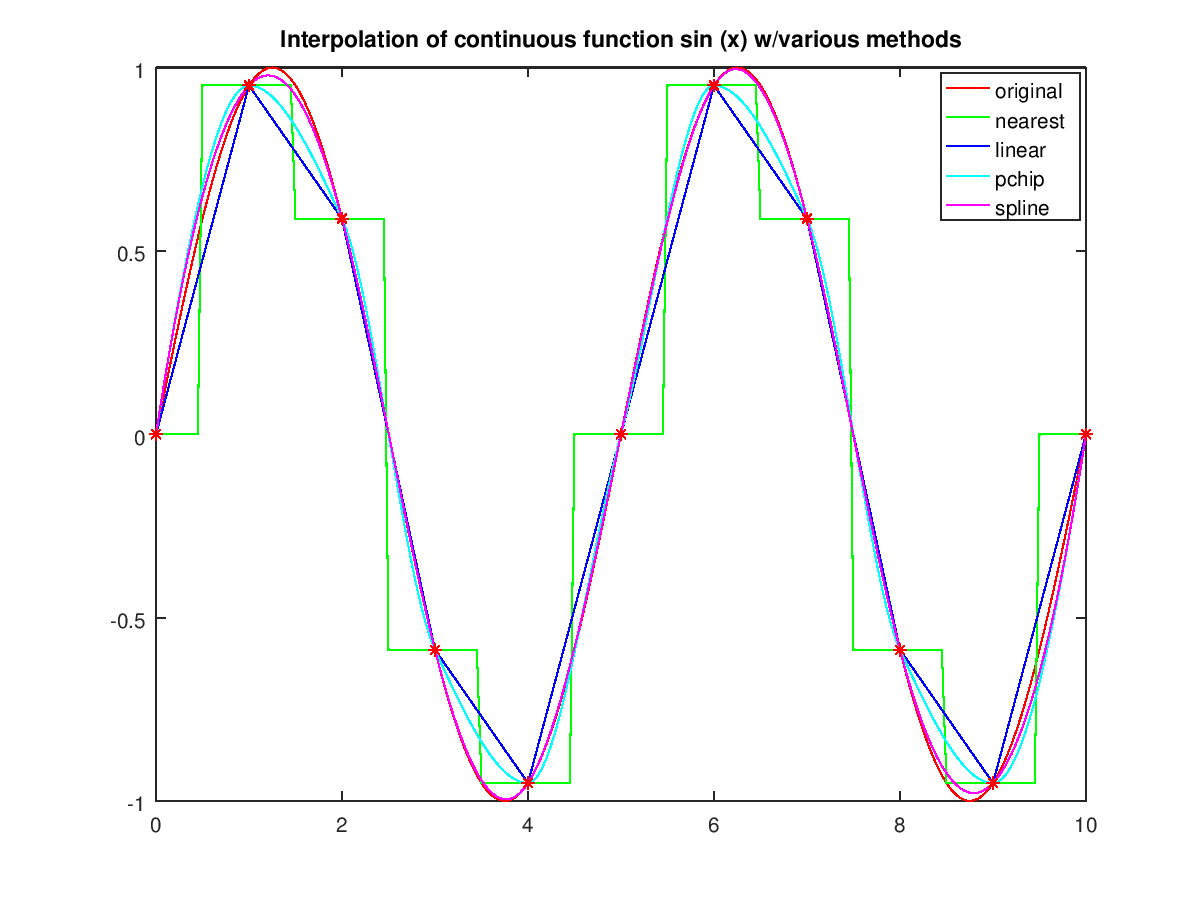
For the ' spline' method, interp1 calls a function spline that uses the M-files ppval, mkpp, and unmkpp. The ' nearest', ' linear' and ' cubic' methods have fairly straightforward implementations. Then the population in 1975, obtained by table lookup within the matrix tab, isĪlgorithm The interp1 command is a MATLAB M-file. If a portion of the census data is stored in a single 5-by-2 table, Sometimes it is more convenient to think of interpolation in table lookup terms where the data are stored in a single table. Now interpolate within the data at every year from 1900 to 2000, and plot the result. The expression interp1(t,p,1975) interpolates within the census data to estimate the population in 1975. P = Described in table lookup terms, the table is tab = and interp1 looks up the elements of xi in x, and, based upon their locations, returns values yi interpolated within the elements of y.Įxamples Here are two vectors representing the census years from 1900 to 1990 and the corresponding United States population in millions of people. Interpolation is the same operation as table lookup. This is shown below, along with the relationship between vectors x, Y, xi, and yi. It finds values of a one-dimensional function f(x) underlying the data at intermediate points. The interp1 command interpolates between data points. For faster interpolation when x is equally spaced, use the methods '* linear', '* cubic', '* nearest', or '* spline'. 'spline' for cubic spline interpolationĪll the interpolation methods require that x be monotonic.'nearest' for nearest neighbor interpolation.Out of range values are returned as NaNs. If Y is a matrix, then the interpolation is performed for each column of Y and yi will be length(xi)-by- size(Y,2). The vector x specifies the points at which the data Y is given.
Returns vector yi containing elements corresponding to the elements of xi and determined by interpolation within vectors x and Y. One-dimensional data interpolation (table lookup) Interp1 (MATLAB Function Reference) MATLAB Function Reference


 0 kommentar(er)
0 kommentar(er)
